Hauptinhalt
Research Topics
Rogue waves and caustics formation for two-dimensionally propagating waves
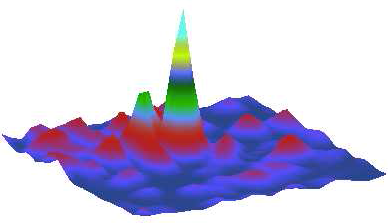
Water waves propagating in the ocean over a seafloor with a spatially varying depth experience a distortion of the wave front and eventually the formation of caustics. Similar effects are well-known for light, remember the bright spots at the bottom of a swimming pool when illuminated by the sun from above. This enhances the probability for the formation of extremely high waves, known as freak or monster waves, by orders of magnitude [1]. We studied the formation of caustics in a setup, where the water waves were replaced by microwaves and the ocean by a flat, quasi-two-dimensional microwave resonator. Statistically distributed obstacles as spherical caps cared for the distortion of the wave front [2].
Literature:
[1] R. Höhmann, U. Kuhl, H.-J. Stöckmann, L. Kaplan, and E. J. Heller, “Freak waves in the linear regime: A microwave study,” Phys. Rev. Lett. 104, 093901 (2010).
(link: http://doi.org/10.1103/PhysRevLett.104.093901)
(free available at: arXiv:0909.0847 link: https://arXiv.org/abs/0909.0847)
[2] S. Barkhofen, J. J. Metzger, R. Fleischmann, U. Kuhl, and H.-J. Söckmann, “Experimental observation of a fundamental length scale of waves in random media,” Phys. Rev. Lett. 111, 183902 (2013).
(link: http://doi.org/10.1103/PhysRevLett.111.183902)
(free available at: arXiv:1308.1583 link: https://arXiv.org/abs/1308.1583)
Simulations of spin 1/2 systems in microwave networks

universal properties of chaotic systems are well reproduced by the corresponding properties of random matrix ensembles. Depending on the symmetry with respect to time reversal there are three universality classes: Systems with time-reversal invariance (TRI) and no spin 1/2 can be described by real symmetric matrices giving rise to the Gaussian orthogonal ensemble. Systems with broken TRI are described by Hermitian but not real matrices leading to the Gaussian unitary ensemble. For both ensembles there had been numerous experimental realizations in the past. For spin 1/2 systems with TRI, described by the Gaussian symplectic ensemble, there had been no systematic study up to now. We performed experiments in microwave networks with a particular symmetry simulating a spin 1/2 system. The degenerate Kramers doublets characteristic for such a symmetry could be clearly observed as well as their splitting when lifting the symmetry [1] (see also photo). In these networks one can also study conductance using the Büttiker relation between conductance and transmission. We have used this analogy to study the transmission in three terminal graphs. Transmission studies had been performed in microwave graphs with orthogonal, unitary, and symplectic symmetry, allowing for a first experimental test of scattering theory for the symplectic case [2].
Literature:
[1] A. Rehemanjiang, M. Allgaier, C. H. Joyner, S. Müller, M. Sieber, U. Kuhl, and H.-J. Stöckmann, “Microwave realization of the gaussian symplectic ensemble,” Phys. Rev. Lett. 117, 064101 (2016).
(link: http://doi.org/10.1103/PhysRevLett.117.064101)
(free available at: arXiv:1601.00467 link: https://arxiv.org/abs/1601.00467)
[2] A. M. Martinez-Arguello, A Rehemanjiang, M Martinez-Mares, J. A. Mendez-Bermudez, H.-J. Stöckmann, and U. Kuhl, “Transport studies in three-terminal microwave graphs with orthogonal, unitary, and symplectic symmetry,” Phys. Rev. B 98, 075311 (2018).
(link: http://doi.org/10.1103/PhysRevB.98.075311
(free available at: arXiv:1808.02852 link: https://arxiv.org/abs/1808.02852)
Wave front shaping in open systems
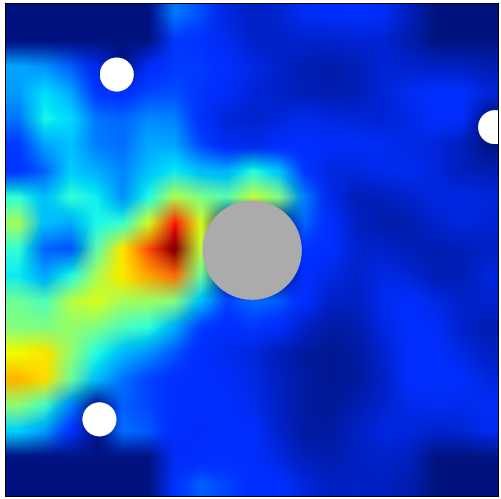
Non-Hermitian wave engineering has recently emerged as an exciting new field. In this subject the incident wave is shaped in such a way that the finally excited wave field or wave transport generate the desired properties. Using spatial light modulators one can perform imaging through tissues, focussing light on tumor cells etc. We have a setup in the microwave regime using IQ-modulators to design the incident waves at wish. By this we could produce particle like scattering states, where the excited wave field inside the system follows the shortest classical trajectory connecting the transmitter to the receiver [1]. This is done by injecting the eigenstate of the Wigner-Smith time delay operator. This state is stable against perturbations and broad band as well, thus a good candidate to perform communication in complex systems. Another possibility is to focus onto a moving scatterer inside a diffusive medium, by injecting the eigenstate of the generalized Wigner-Smith operator, where the derivative is taken on the position of the scatterer instead of the frequency [2] (see also photo).
Literature:
[1] J. Böhm, A. Brandstötter, P. Ambichl, S. Rotter, and U. Kuhl, “In situ realization of particlelike scattering states in a microwave cavity,” Phys. Rev. A 97, 021801(R) (2018).
(link: http://doi.org/10.1103/PhysRevA.97.021801)
(free available at: arXiv:1706.08926 link: https://arxiv.org/abs/1706.08926)
[2] P. Ambichl, A. Brandstötter, J. Böhm, M. Kühmayer, U. Kuhl, and S. Rotter, “Focusing inside disordered media with the generalized Wigner-Smith operator,” Phys. Rev. Lett. 119, 033903 (2017).
(link: http://doi.org/10.1103/PhysRevLett.119.033903)
(free available at: arXiv:1703.07250 link: https://arxiv.org/abs/1703.07250
Tight binding experiment (Topologie, Graphene, Molecules)

coupled high index cylindrical resonators we are able to realize one- and two-dimensional tight binding systems [1]. This allows us to investigate chains with special topological properties (like the SSH model) or the band structures of graphene and its electrical transport properties. At the K, K' points in the Brillouin zone the graphene band structure exhibits a linear energy momentum dispersion relation as it is typical for the Dirac equation. This results in a double-conical band structure at the K, K' points known as Dirac cones. This opens the possibility to study relativistic quantum mechanics at non-relativistic energies. We could for examples investigate the dependence of the Dirac cones on stress applied to the artificial graphene [2]. Due to topological features in graphene nanoribbons edge states are present and transport can be present even if the bulk material has a band gap. In this case the conductance is governed by the topological edge states. Additionally, questions on spectra of molecules like benzene or poly-acetylene are accessible.
Literature:
[1] U. Kuhl, S. Barkhofen, T. Tudorovskiy, H.-J. Stöckmann, T. Hossain, L. de Forges de Parny, and F. Mortessagne, “Dirac point and edge states in a microwave realization of tight-binding graphene-like structures,” Phys. Rev. B 82, 094308 (2010).
(link: http://doi.org/10.1103/PhysRevB.82.094308)
(free available at: arXiv:1006.0901 link: https://arxiv.org/abs/1006.0901)
[2] M. Bellec, U. Kuhl, G. Montambaux, and F. Mortessagne, “Topological transition of Dirac points in a microwave experiment,” Phys. Rev. Lett. 110, 033902 (2013).
(link: http://doi.org/10.1103/PhysRevLett.110.033902)
(free available at: arXiv:1210.4642 link: https://arxiv.org/abs/1210.4642)
Microwave experiments on scattering theory, effective Hamiltonian approach, random matrix theory, and Anderson localization
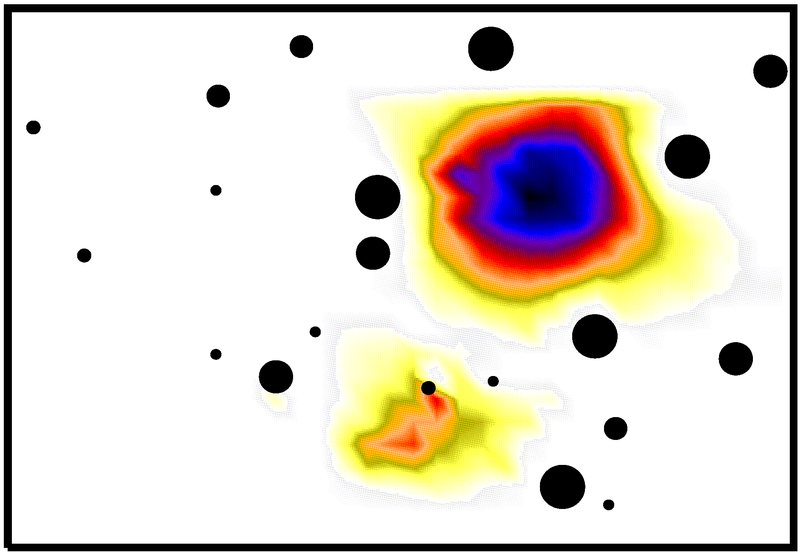
a measurement on a wave system always disturbs the system and the measured quantities have to be described by scattering theory. One way for the description of open quantum system successfully uses the concept of the effective Hamiltonian, which takes into account the coupling to the environment [1,2]. The concept can be extended to classical waves. Experimentally, classical waves are very convenient as they allow to control boundaries, coupling and absorption. We explore microwaves scattering to investigate properties of open systems which can be described by an effective Hamiltonian. This ranges from spectral properties like modifications to level dynamics, width distribution and coupling fidelity to spatial properties like intensity distributions and complexness parameter which describes the non-orthogonality of eigenfunctions.
Another wave phenomena occurring in disorderd systems is the localization of waves. Additionally, correlations in the disorder potential can be used to increase or decrease localization length, which we have found experimentally [3].
Literature:
[1] U. Kuhl, M. Martinez-Mares, R. A. Mendez-Sanchez, and H.-J. Stöckmann, “Direct processes in chaotic microwave cavities in the presence of absorption,” Phys. Rev. Lett. 94, 144101 (2005).
(link: http://doi.org/10.1103/PhysRevLett.94.144101)
(free available at: arXiv:0407197 link: https://arxiv.org/abs/cond-mat/0407197)
[2] U. Kuhl, O. Legrand, and F. Mortessagne, “Microwave experiments using open chaotic cavities in the realm of the effective Hamiltonian formalism,” Fortschritte der Physik 61, 404 (2013).
(link: http://doi.org/10.1002/prop.201200101)
(free available at: HAL: hal-00745609 link: https://hal.archives-ouvertes.fr/hal-00745609)
[3] U. Kuhl, F. M. Izrailev, A. A. Krokhin, and H.-J. Stöckmann, “Experimental observation of the mobility edge in a waveguide with correlated disorder,” Appl. Phys. Lett. 77, 633 (2000).
(link: http://doi.org/10.1063/1.127068)
(free available at: arXiv: arxiv-cond-mat9911158 link: http://arxiv.org/abs/cond-mat/9911158v1)