Hauptinhalt
Fortgeschrittenenpraktikum
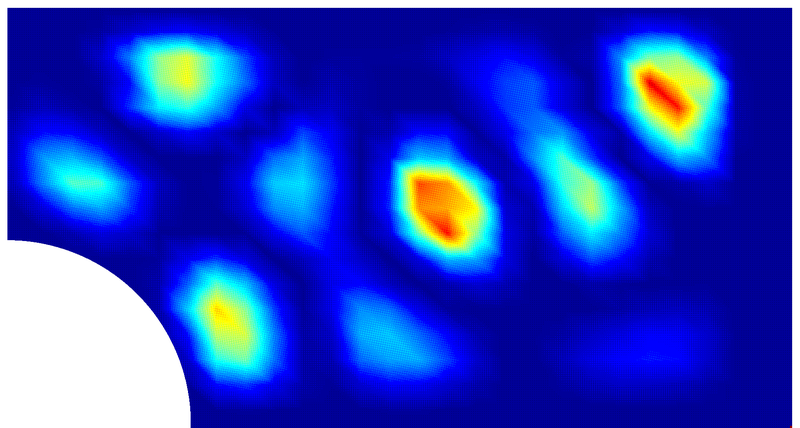
In classical dynamics a chaotic system is characterized by an exponential sensitivity on the initial conditions of trajectories. Quantum-mechanically this definition breaks down. There are no longer trajectories, and initial conditions can be described only within the limits of the uncertainty relation. Instead one has to look in the spectra and wave-functions for the fingerprints of chaos. Billiard systems, in this context just single particles moving in the plane and experiencing specular reflects at the boundary, are ideal candidates to study such questions. Furthermore, there is a one-to-one correspondence between the stationary Schrödinger and the Helmholtz equation, allowing for an experimental access to "quantum chaos" by means of classical waves.
In the students set-up differently shaped microwave resonators are used. The students take the spectra of both one regular and one chaotic resonator and measure a wave-function for each of them. The distance distributions of nearest eigenresonances will show up to be a sensitive tool to discriminate between regular and chaotic systems. The wave-functions, too, will show characteristic differences between the two.
The “Praktikumsanleitung” can be downloaded here