Hauptinhalt
Interessantes zum Logo des Fachbereichs
Das Logo des Fachbereichs repräsentiert die beiden Fachgebiete Mathematik und Informatik:

- Das gezeigte Objekt, die Sextik von Barth, ist eine algebraische Fläche und damit ein Untersuchungsgegenstand der algebraischen Geometrie.
- Die Darstellung der Fläche unter Berücksichtigung von Vorder- und Hintergrund, Perspektive und Beleuchtungseffekten ist eine anspruchsvolle Aufgabe der Graphikprogrammierung.
Beide Gebiete, die algebraische Geometrie und die Graphikprogrammierung, sind am Fachbereich durch Experten vertreten.
Genaueres zur algebraischen Geometrie
Bei der gezeigten Fläche handelt es sich um eine algebraische Fläche vom Grad 6 (eine Sextik) im dreidimensionalen projektiven Raum, die als Lösung einer algebraischen Gleichung definiert ist. Sie wurde im Jahr 1996 von W. Barth entdeckt. Ihre Besonderheit liegt darin, dass sie 65 Knoten hat. (Im Bild sind dies diejenigen Punkte auf der Fläche, in denen die Fläche »zusammengeschnürt« erscheint, nicht alle 65 Knoten sind im Bild sichtbar.) Erstaunlich ist, dass keine Sextik mehr als 65 Knoten haben kann - Barths Fläche stellt also den »maximalen Fall« dar. Sie ist die erste bekannte Fläche dieses Typs.
Für Experten:
$$4\big(\Phi^2x^2-y^2\big)\big(\Phi^2y^2-z^2\big)\big(\Phi^2z^2-x^2\big)-\big(1+2\Phi\big)\big(x^2+y^2+z^2-w^2\big)^2w^2 = 0$$
$$\Phi = \frac{\sqrt{5}+1}{2}$$
In homogenen Koordinaten ist die Fläche durch die obige Gleichung gegeben. Die Zahl Φ, die in der Gleichung vorkommt, ist übrigens der Goldene Schnitt. Sie spielt in vielen Zusammenhängen eine große Rolle - in der Mathematik, aber auch in Architektur und Malerei. Nur wenn man diesen Wert in der Gleichung der Fläche verwendet, hat sie wirklich 65 Knoten. Erstaunlich.
Genaueres zur Graphikprogrammierung
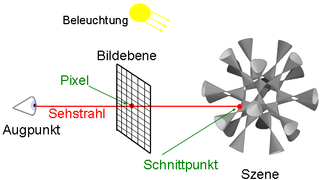
Die zur Darstellung der Fläche benutzte Methode ist das Raytracing, die „Strahlverfolgung“, ein aufwändiges Verfahren, das bei komplizierten Objekten wie der Sextik zu sehr guten Resultaten führt. Man verfolgt dabei einen Sehstrahl vom Auge des Betrachters aus in die darzustellende Szene. Durch die Wahl eines Augpunktes - der Position des Betrachters - und der Bildebene ist die Perspektive festgelegt. Danach wird zu Strahlen, die vom Augpunkt aus durch die einzelnen Pixel der Bildebene gehen, jeweils der erste Schnittpunkt mit einem Objekt der Szene berechnet und daraus die Grundfarbe des Pixels bestimmt. Damit kann bereits der vom Augpunkt aus sichtbare Teil der Szene auf der Bildebene dargestellt werden.
Für einen realistischen Eindruck müssen zusätzlich Beleuchtungseffekte berücksichtigt werden. Zunächst müssen die Hintergrundhelligkeit, die Beleuchtung durch ein oder mehrere Lichtquellen und die Oberflächeneigenschaften der Objekte der Szene festgelegt werden. Außerdem muss die indirekte Beleuchtung durch andere Komponenten der Szene berücksichtigt werden. Zu diesem Zweck werden von dem ursprünglichen Schnittpunkt aus Sekundärstrahlen verfolgt (diese sind in dem Bild oben nicht eingezeichnet). Deren Richtung ergibt sich aus dem Winkel zwischen dem ursprünglichen Strahl und der Oberflächen-normalen im Auftreffpunkt. Die Sekundärstrahlen werden verfolgt bis sie wiederum ein Objekt der Szene erreichen. Dieser Vorgang wird bis zu einer gewissen Rekursionstiefe wiederholt. Durch die Verfolgung von Sekundärstrahlen verändert sich die ursprünglich bestimmte Grundfarbe des Pixels, man erhält auf diese Weise Spiegelungs-Effekte innerhalb der Szene. Die Oberflächeneigenschaften der Objekte der Szene bestimmen die Farbe der Objekte und ob die jeweilige Oberfläche einfallendes Licht eher diffus oder eher spiegelnd reflektiert. Eine einzelne Reflexion berechnet sich aus dem Winkel zwischen Strahl und Oberflächennormalen im Auftreffpunkt sowie den angenommenen Eigenschaften des Objekts. Der realistische Eindruck wird durch die Verfolgung von Sekundärstrahlen über mehrere Generationen erhöht, was aber zu dem hohen Rechenaufwand des Verfahrens beiträgt.

Im Sommer 2013 wurde in der Mathematischen Modellsammlung des Fachbereichs das erste physikalische Modell der Barth'schen Sextik angefertigt, bei dem die Singularitaeten nicht geglaettet sind. Dazu wurden die einzelnen Teile mit Hilfe eines 3-D-Plotters aus weissem Kunststoff gedruckt, per Hand auf Draht aufgezogen und lackiert. Die Fotoserie zeigt die einzelnen Arbeitsschritte sowie das fertige Modell, das nun in einer Vitrine vor der Bibliothek des Fachbereichs steht.
Siehe auch:
- Barth, W: Two projective surfaces with many nodes, admitting the symmetries of the icosahedron. J. Algebraic Geometry 5, 173-186 (1996)
- Raytracing in Wikipedia
- H.P. Gumm und M. Sommer: Einführung in die Informatik, Oldenbourg Verlag, 10. Auflage, 2012: http://www.informatikbuch.de/