High-Performance Computing of Flow and Transport

Accurate prediction and optimization of transport processes in porous media require a qualitative and quantitative understanding of underlying physical phenomena. The complexity of the pore geometry and topological pore connectivity makes it impossible to apply analytical methods for solution of the generic transport equations. As a result, it is necessary to employ numerical methods to solve these equations, or, in other words, to perform computer simulations. The structure of the pore space requires utilization of exceptional computational resources and advanced numerical techniques to perform the pore-scale modeling of transport in macroscopically representative samples of porous media. For this purpose, we employ a comprehensive modeling approach that combines three-dimensional pore-scale simulations of fluid flow by a lattice-Boltzmann method with simulations of advective–diffusive transport based on a random-walk particle-tracking technique.

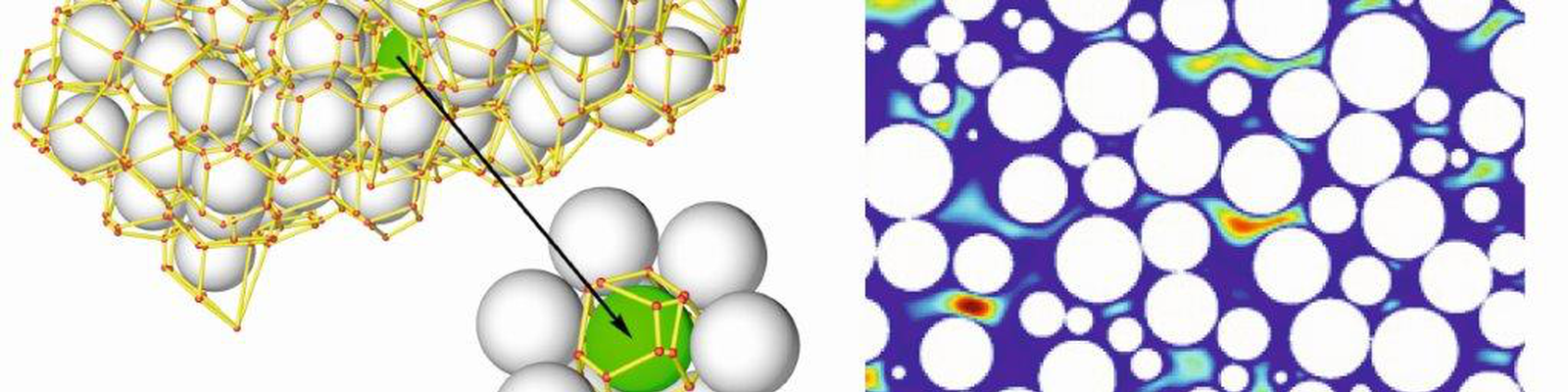
Lattice-Boltzmann Method (LBM). A lattice-Boltzmann method is a mesoscopic approach based on the connection between microscopic (molecular kinetics) and macroscopic (phenomenological) descriptions of a fluid. The macroscopic fluid dynamics is approximated by synchronous interactions between fictitious fluid particles on a regular lattice based on the idea that fluid flow is determined mainly by the collective behavior of many molecules and not by detailed molecular interactions. The kinetics of an ensemble of fictitious fluid particles is described in terms of the discrete single-particle velocity distribution function fi(r,t), which defines the probability density of particles with a discrete velocity ei around the space-time point (r,t). The time-evolution of fi(r,t) is described by the discrete (lattice) Boltzmann equation. Local values of the fluid density and flow velocity are obtained from the first-order and second-order statistical moments of fi(r,t) in corresponding lattice units. At present, the LBM is the best tool for pore-scale simulations of fluid flow in porous media, particularly due to its ability to accurately handle complex solid–liquid interfaces (like those found in random porous media) without need for simplifications or extensive meshing. Inherent parallelism of the LBM allows its straightforward implementation at high-performance computational systems (supercomputers) and large-scale calculation of the pore-scale flow velocity with a fine resolution. For instance, we resolved the 3D velocity field in cylindrical random packings of spherical particles (i.e., spheres packed randomly into a cylindrical column) with dimension of 30 dp (diameter) x 9830 dp (length), where dp is the particle diameter, having a spatial resolution of dp/30. An LBM simulation for the corresponding discrete lattice composed of about 1011 nodes required ~30 TB memory and ~0.6 hours on 98,304 processor cores of a BlueGene/P system at FZJ (Forschungszentrum Jülich, Germany).

Random-Walk Particle-Tracking (RWPT) Method. This approach to simulate advective–diffusive transport is based on the equivalence between the phenomenological advection–diffusion equation and the stochastic differential equation describing the time-evolution of the tracer position, resulting from drift due to the underlying local flow field (commonly calculated with the LBM) and Brownian motion due to molecular diffusion. For each elementary time step, the displacement of a tracer is determined as the sum of convective and diffusive motions. During transport simulations, the coordinates of every tracer from a large ensemble (several millions) are monitored. It allows to calculate statistical moments of the tracer displacements, which can be related to macroscopic transport characteristics, such as the effective diffusion coefficient, the hydrodynamic dispersion coefficient, and the retention factor (that is, how strongly a species is retained by its interaction with the surface of a material). Advantages of the RWPT approach are mass conservation, absence of numerical dispersion, as well as simplicity of the program realization and its further parallelization.

We have used the combined LBM–RWPT simulation approach to determine mass transport properties of a variety of porous media, with an emphasis on establishing quantitative morphology–transport relationships for targeted material design. Specifically, the studied porous media include