Hauptinhalt
Bayes-Statistik und hierarchische Modellierung
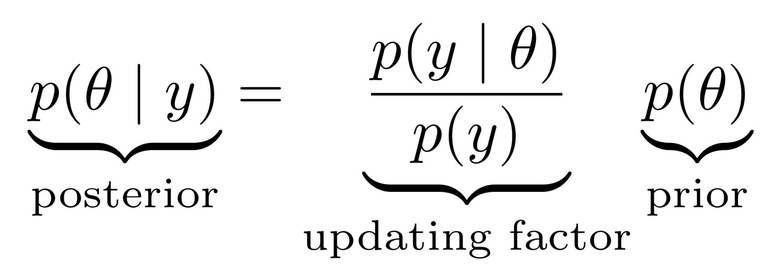
In der psychologischen Forschung wird zunehmend Bayes-Statistik eingesetzt um statistische Schlussfolgerungen zu ziehen. Im Gegensatz zur klassischen, frequentistischen Statistik erlaubt die Bayes-Statistik eine intuitivere Interpretation von Parameter-Schätzern und Unsicherheitsintervallen (z.B.: „die Differenz zweier Mittelwerte ist mit 95% Wahrscheinlichkeit im Intervall [0.24, 0.36]“) sowie von Hypothesentests (z.B.: „für die beobachteten Daten ist die Nullhypothese 10 mal wahrscheinlicher als die Alternativhypothese“). Um solche Aussagen über die „Posterior Verteilung“ (d.h. über die Verteilung von Parametern gegeben die beobachteten Daten) machen zu können, ist es notwendig, ein statistisches Modell zu definieren (die „Likelihood Funktion“) sowie Vorannahmen über plausible Werte der Parameter zu machen (die „Prior“ Verteilung).
In unserer Forschung nutzen wir Bayes-Statistik für die statistische und kognitive Modellierung und den Test psychologischer Theorien, insbesondere im Rahmen hierarchischer Modelle, die getrennte Parameter für verschiedene Personen annehmen. Darüber hinaus interessieren wir uns für die Implementierung dieser Methoden in der Statistik-Software R sowie mögliche Fehler, die bei der Anwendung passieren können. Weiterhin ist es von Interesse, Bayes-Statistik und frequentistische Methoden gegenüberzustellen um Empfehlungen für die Anwendung in der Praxis zu geben.
Bayes'sche Modellierung:
- Siepe, B. S., Kloft, M., & Heck, D. W. (in press). Bayesian estimation and comparison of idiographic network models. Psychological Methods. https://doi.org/10.1037/met0000672
- Kloft, M., Hartmann, R., Voss, A., & Heck, D. W. (2023). The Dirichlet Dual Response Model: An Item Response Model for Continuous Bounded Interval Responses. Psychometrika. https://doi.org/10.1007/s11336-023-09924-7
- Heck, D. W., & Davis-Stober, C. P. (2019). Multinomial models with linear inequality constraints: Overview and improvements of computational methods for Bayesian inference. Journal of Mathematical Psychology, 91, 70-87. https://doi.org/10.1016/j.jmp.2019.03.004
- Heck, D. W. (2019). Accounting for estimation uncertainty and shrinkage in Bayesian within-subject intervals: A comment on Nathoo, Kilshaw, and Masson (2018). Journal of Mathematical Psychology, 88, 27-31. https://doi.org/10.1016/j.jmp.2018.11.002
Bayes Factors zur Modellselektion:
- Heck, D. W., et al. (2022). A review of applications of the Bayes factor in psychological research. Psychological Methods. https://doi.org/10.1037/met0000454
- Heck, D. W. (2024). Invited discussion: Model-averaged credible intervals for point-null hypotheses. Bayesian Analysis, 19, 946–950. https://doi.org/10.1214/23-BA1397
- Heck, D. W., & Bockting, F. (2021). Benefits of Bayesian model averaging for mixed-effects modeling. Computational Brain & Behavior. https://doi.org/10.1007/s42113-021-00118-x
- Heck, D. W. (2019). A caveat on the Savage-Dickey density ratio: The case of computing Bayes factors for regression parameters. British Journal of Mathematical and Statistical Psychology, 72, 316-333. https://doi.org/10.1111/bmsp.12150
- Heck, D. W., & Wagenmakers, E. (2016). Adjusted priors for Bayes factors involving reparameterized order constraints. Journal of Mathematical Psychology, 73, 110-116. https://doi.org/10.1016/j.jmp.2016.05.004
- Heck, D. W., Wagenmakers, E., & Morey, R. D. (2015). Testing order constraints: Qualitative differences between Bayes factors and normalized maximum likelihood. Statistics & Probability Letters, 105, 157-162. https://doi.org/10.1016/j.spl.2015.06.014